Alternating current (AC) circuits, impedance, phase relations, resonance and RMS quantities. AC electricity is ubiquitous not only in the supply of power, but in electronics and signal processing. - If impedance is voltage over current, why is it different from resistance?
- What are RMS values?
- How can you have 100 volts across a capacitor, 100 volts across an inductor, and 10 volts across the two of them in series?
- What does it mean to say that current and voltage are out of phase?
- Why does the ratio of voltage to current in capacitors and inductors depend on frequency?
| 
The voltage across a resistor (upper trace) and an inductor
(lower trace) in series. Note the phase difference. |
This page provides answers to these questions and more. We introduce the voltage-current relations for resistors, capacitors and inductors separately using animations to show the time-varying nature, and why frequency is important. Then we combine the components in series and parallel.| Sub-headings on this page are: | There are separate pages on |
But first, why study AC circuits? You probably live in a house or appartment with sockets that deliver AC. Your radio, television and portable phone receive it, using (among others) circuits like those below. As for the computer you're using to read this, its signals are not ordinary sinusoidal AC, but, thanks to Fourier's theorem, any varying signal may be analysed in terms of its sinusoidal components. So AC signals are almost everywhere. And you can't escape them, because even the electrical circuits in your brain use capacitors and resistors.
Some terminologyFor brevity, we shall refer to electrical potential difference as voltage. Throughout this page, we shall consider voltages and currents that vary sinusoidally with time. We shall use lower case v and i for the voltage and current when we are considering their variation with time explicitly. The amplitude or peak value of the sinusoidal variation we shall represent by Vm and Im, and we shall use V = Vm/√2 and I = Im/√2 without subscripts to refer to the RMS values. For an explanation of RMS values, see Power and RMS values. For the origin of the sinusoidally varying voltage in the mains supply, see Motors and generators.So for instance, we shall write: v = v(t) = Vm sin (ωt + φ)
i = i(t) = Im sin (ωt). where ω is the angular frequency. ω = 2πf, where f is the ordinary or cyclic frequency. f is the number of complete oscillations per second. φ is the phase difference between the voltage and current. We shall meet this and the geometrical significance of ω later.
Resistors and Ohm's law in AC circuitsThe voltage v across a resistor is proportional to the current i travelling through it. (See the page on drift velocity and Ohm's law.) Further, this is true at all times: v = Ri. So, if the current in a resistor isi = Im . sin (ωt) , we write:
v = R.i = R.Im sin (ωt)
v = Vm. sin (ωt) where
Vm = R.Im So for a resistor, the peak value of voltage is R times the peak value of current. Further, they are in phase: when the current is a maximum, the voltage is also a maximum. (Mathematically, φ = 0.) The first animation shows the voltage and current in a resistor as a function of time. The rotating lines in the right hand part of the animation are a very simple case of a phasor diagram (named, I suppose, because it is a vector representation of phase). With respect to the x and y axes, radial vectors or phasors representing the current and the voltage across the resistance rotate with angular velocity ω. The lengths of these phasors represent the peak current Im and voltage Vm. The y components are Im sin (ωt) = i(t) and voltage Vm sin (ωt)= v(t). You can compare i(t) and v(t) in the animation with the vertical components of the phasors. The animation and phasor diagram here are simple, but they will become more useful when we consider components with different phases and with frequency dependent behaviour. (See Physclips for a comparison of simple harmonic motion and circular motion)
What are impedance and reactance?Circuits in which current is proportional to voltage are called linear circuits. (As soon as one inserts diodes and transistors, circuits cease to be linear, but that's another story.) The ratio of voltage to current in a resistor is its resistance. Resistance does not depend on frequency, and in resistors the two are in phase, as we have seen in the animation. However, circuits with only resistors are not very interesting.In general, the ratio of voltage to current does depend on frequency and in general there is a phase difference. So impedance is the general name we give to the ratio of voltage to current. It has the symbol Z. Resistance is a special case of impedance. Another special case is that in which the voltage and current are out of phase by 90°: this is an important case because when this happens, no power is lost in the circuit. In this case where the voltage and current are out of phase by 90°, the ratio of voltage to current is called the reactance, and it has the symbol X. We return to summarise these terms and give expressions for them below in the section Impedance of components, but first let us see why there are frequency dependence and phase shifts for capacitors and for inductors.
Capacitors and chargingThe voltage on a capacitor depends on the amount of charge you store on its plates. The current flowing onto the positive capacitor plate (equal to that flowing off the negative plate) is by definition the rate at which charge is being stored. So the charge Q on the capacitor equals the integral of the current with respect to time. From the definition of the capacitance,vC = q/C, so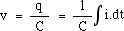
Now remembering that the integral is the area under the curve (shaded blue), we can see in the next animation why the current and voltage are out of phase.Once again we have a sinusoidal current i = Im . sin (ωt), so integration gives (The constant of integration has been set to zero so that the average charge on the capacitor is 0). Now we define the capacitive reactance XC as the ratio of the magnitude of the voltage to magnitude of the current in a capacitor. From the equation above, we see that XC = 1/ωC. Now we can rewrite the equation above to make it look like Ohm's law. The voltage is proportional to the current, and the peak voltage and current are related by Note the two important differences. First, there is a difference in phase: the integral of the sinusoidal current is a negative cos function: it reaches its maximum (the capacitor has maximum charge) when the current has just finished flowing forwards and is about to start flowing backwards. Run the animation again to make this clear. Looking at the relative phase, the voltage across the capacitor is 90°, or one quarter cycle, behind the current. We can see also see how the φ = 90° phase difference affects the phasor diagrams at right. Again, the vertical component of a phasor arrow represents the instantaneous value of its quanitity. The phasors are rotating counter clockwise (the positive direction) so the phasor representing VC is 90° behind the current (90° clockwise from it). Recall that reactance is the name for the ratio of voltage to current when they differ in phase by 90°. (If they are in phase, the ratio is called resistance.) Another difference between reactance and resistance is that the reactance is frequency dependent. From the algebra above, we see that the capacitive reactance XC decreases with frequency . This is shown in the next animation: when the frequency is halved but the current amplitude kept constant, the capacitor has twice as long to charge up, so it generates twice the potential difference. The blue shading shows q, the integral under the current curve (light for positive, dark for negative). The second and fourth curves show VC = q/C . See how the lower frequency leads to a larger charge (bigger shaded area before changing sign) and therefore a larger VC. Thus for a capacitor, the ratio of voltage to current decreases with frequency. We shall see later how this can be used for filtering different frequencies.
Inductors and the Farady emfAn inductor is usually a coil of wire. In an ideal inductor, the resistance of this wire is negligibile, as is its capacitance. The voltage that appears across an inductor is due to its own magnetic field and Faraday's law of electromagnetic induction. The current i(t) in the coil sets up a magnetic field, whose magnetic flux φB is proportional to the field strength, which is proportional to the current flowing. (Do not confuse the phase φ with the flux φB.) So we define the (self) inductance of the coil thus:Faraday's law gives the emf EL = - dφB/dt. Now this emf is a voltage rise, so for the voltage drop vL across the inductor, we have:Again we define the inductive reactance XL as the ratio of the magnitudes of the voltage and current, and from the equation above we see that XL = ωL. Again we note the analogy to Ohm's law: the voltage is proportional to the current, and the peak voltage and currents are related by Remembering that the derivative is the local slope of the curve (the purple line), we can see in the next animation why voltage and current are out of phase in an inductor. Again, there is a difference in phase: the derivative of the sinusoidal current is a cos function: it has its maximum (largest voltage across the inductor) when the current is changing most rapidly, which is when the current is intantaneously zero. The animation should make this clear. The voltage across the ideal inductor is 90° ahead of the current, (ie it reaches its peak one quarter cycle before the current does). Note how this is represented on the phasor diagram. Again we note that the reactance is frequency dependent XL = ωL. This is shown in the next animation: when the frequency is halved but the current amplitude kept constant, the current is varying only half as quickly, so its derivative is half as great, as is the Faraday emf. For an inductor, the ratio of voltage to current increases with frequency, as the next animation shows.
Impedance of componentsLet's recap what we now know about voltage and curent in linear components. The impedance is the general term for the ratio of voltage to current. Resistance is the special case of impedance when φ = 0, reactance the special case when φ = ± 90°. The table below summarises the impedance of the different components. It is easy to remember that the voltage on the capacitor is behind the current, because the charge doesn't build up until aas been flowing for a while. The same information is given graphically below. It is easy to remember the frequency dependence by thinking of the DC (zero frequency) behaviour: at DC, an inductance is a short circuit (a piece of wire) so its impedance is zero. At DC, a capacitor is an open circuit, as its circuit diagram shows, so its impedance goes to infinity.
RC Series combinationsWhen we connect components together, Kirchoff's laws apply at any instant. So the voltage v(t) across a resistor and capacitor in series is justvseries(t) = vR(t) + vC(t) however the addition is complicated because the two are not in phase. The next animation makes this clear: they add to give a new sinusoidal voltage, but the amplitude is less than VmR(t) + VmC(t). Similarly, the AC voltages (amplitude times √2) do not add up. This may seem confusing, so it's worth repeating:vseries = vR + vC but
Vseries < VR + VC. This should be clear on the animation and the still graphic below: check that the voltages v(t) do add up, and then look at the magnitudes. The amplitudes and the RMS voltages V do not add up in a simple arithmetical way.
Here's where phasor diagrams are going to save us a lot of work. Play the animation again (click play), and look at the projections on the vertical axis. Because we have sinusoidal variation in time, the vertical component (magnitude times the sine of the angle it makes with the x axis) gives us v(t). But the y components of different vectors, and therefore phasors, add up simply: if rtotal = r1 + r2, then
ry total = ry1 + ry2. So v(t), the sum of the y projections of the component phasors, is just the y projection of the sum of the component phasors. So we can represent the three sinusoidal voltages by their phasors. (While you're looking at it, check the phases. You'll see that the series voltage is behind the current in phase, but the relative phase is somewhere between 0 and 90°, the exact value depending on the size of VR and VC. We'll discuss phase below.)Now let's stop that animation and label the values, which we do in the still figure below. All of the variables (i, vR, vC, vseries) have the same frequency f and the same angular frequency ω, so their phasors rotate together, with the same relative phases. So we can 'freeze' it in time at any instant to do the analysis. The convention I use is that the x axis is the reference direction, and the reference is whatever is common in the circuit. In this series circuit, the current is common. (In a parallel circuit, the voltage is common, so I would make the voltage the horizontal axis.) Be careful to distinguish v and V in this figure! 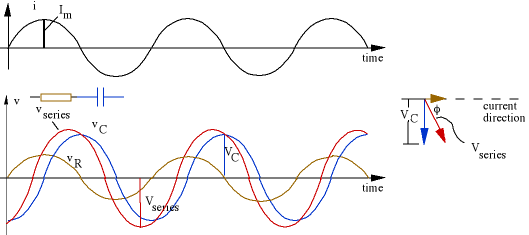
(Careful readers will note that I'm taking a shortcut in these diagrams: the size of the arrows on the phasor diagrams are drawn the same as the amplitudes on the v(t) graphs. However I am just calling them VR, VC etc, rather than VmR, VmR etc. The reason is that the peak values (VmR etc) are rarely used in talking about AC: we use the RMS values, which are peak values times 0.71. Phasor diagrams in RMS have the same shape as those drawn using amplitudes, but everything is scaled by a factor of 0.71 = 1/√2.)The phasor diagram at right shows us a simple way to calculate the series voltage. The components are in series, so the current is the same in both. The voltage phasors (brown for resistor, blue for capacitor in the convention we've been using) add according to vector or phasor addition, to give the series voltage (the red arrow). By now you don't need to look at v(t), you can go straight from the circuit diagram to the phasor diagram, like this: From Pythagoras' theorem:If we divide this equation by two, and remembering that the RMS value V = Vm/√2, we also get:Now this looks like Ohm's law again: V is proportional to I. Their ratio is the series impedance, Zseries and so for this series circuit,Note the frequency dependence of the series impedance ZRC: at low frequencies, the impedance is very large, because the capacitive reactance 1/ωC is large (the capacitor is open circuit for DC). At high frequencies, the capacitive reactance goes to zero (the capacitor doesn't have time to charge up) so the series impedance goes to R. At the angular frequency ω = ωo = 1/RC, the capacitive reactance 1/ωC equals the resistance R. We shall show this characteristic frequency* on all graphs on this page.* Let's check the units: it should be quick. First, a radian is the ratio of an arc to a radius, so it is a pure number. R is in ohms, and we can use Ohm's law (V = IR) and the definition of current (I = dQ/dt) to write ohm = volt/ampere = volt/(coulomb/second) = volt*second/coulomb. C (charge per unit voltage) is in farads (coulomb/volt), so RC has the units of (volt*second/coulomb)(coulomb/volt) = second. See, it was quick: it only took us 30 ohm.farads! Remember how, for two resistors in series, you could just add the resistances: Rseries = R1 + R2 to get the resistance of the series combination. That simple result comes about because the two voltages are both in phase with the current, so their phasors are parallel. Because the phasors for reactances are 90° out of phase with the current, the series impedance of a resistor R and a reactance X are given by Pythagoras' law: Ohm's law in AC. We can rearrange the equations above to obtain the current flowing in this circuit. Alternatively we can simply use the Ohm's Law analogy and say that I = Vsource/ZRC. Either way we getwhere the current goes to zero at DC (capacitor is open circuit) and to V/R at high frequencies (no time to charge the capacitor).So far we have concentrated on the magnitude of the voltage and current. We now derive expressions for their relative phase, so let's look at the phasor diagram again. From simple trigonometry, the angle by which the current leads the voltage isHowever, we shall refer to the angle φ by which the voltage leads the current. The voltage is behind the current because the capacitor takes time to charge up, so φ is negative, ieφ = -tan-1 (1/ωRC) = tan-1 (1/2πfRC). .gif) (You may want to go back to the RC animation to check out the phases in time.)At low frequencies, the impedance of the series RC circuit is dominated by the capacitor, so the voltage is 90° behind the current. At high frequencies, the impedance approaches R and the phase difference approaches zero. The frequency dependence of Z and φ are important in the applications of RC circuits. The voltage is mainly across the capacitor at low frequencies, and mainly across the resistor at high frequencies. Of course the two voltages must add up to give the voltage of the source, but they add up as vectors.At the frequency ω = ωo = 1/RC, the phase φ = 45° and the voltage fractions are VR/VRC = VC/VRC = 1/2V1/2 = 0.71.So, by chosing to look at the voltage across the resistor, you select mainly the high frequencies, across the capacitor, you select low frequencies. This brings us to one of the very important applications of RC circuits, and one which merits its own page: filters, integrators and differentiators where we use sound files as examples of RC filtering.
RL Series combinationsIn an RL series circuit, the voltage across the inductor is aheadof the current by 90°, and the inductive reactance, as we saw before, is XL = ωL. The resulting v(t) plots and phasor diagram look like this.It is straightforward to use Pythagoras' law to obtain the series impedance and trigonometry to obtain the phase. We shall not, however, spend much time on RL circuits, for three reasons. First, it makes a good exercise for you to do it yourself. Second, RL circuits are used much less than RC circuits. This is because inductors are always* too big, too expensive and the wrong value, a proposition you can check by looking at an electronics catalogue. If you can use a circuit involving any number of Rs, Cs, transistors, integrated circuits etc to replace an inductor, one usually does. The third reason why we don't look closely at RL circuits on this site is that you can simply look at RLC circuits (below) and omit the phasors and terms for the capacitance.* Exceptions occur at high frequencies (~GHz) where only small value Ls are required to get substantial ωL. In such circuits, one makes an inductor by twisting copper wire around a pencil and adjusts its value by squeezing it with the fingers.
RLC Series combinationsNow let's put a resistor, capacitor and inductor in series. At any given time, the voltage across the three components in series, vseries(t), is the sum of these:vseries(t) = vR(t) + vL(t) + vC(t), The current i(t) we shall keep sinusoidal, as before. The voltage across the resistor, vR(t), is in phase with the current. That across the inductor, vL(t), is 90° ahead and that across the capacitor, vC(t), is 90° behind.Once again, the time-dependent voltages v(t) add up at any time, but the RMS voltages V do not simply add up. Once again they can be added by phasors representing the three sinusoidal voltages. Again, let's 'freeze' it in time for the purposes of the addition, which we do in the graphic below. Once more, be careful to distinguish v and V. Look at the phasor diagram: The voltage across the ideal inductor is antiparallel to that of the capacitor, so the total reactive voltage (the voltage which is 90° ahead of the current) is VL - VC, so Pythagoras now gives us:V2series = V2R + (VL - VC)2 Now VR = IR, VL = IXL = ωL and VC = IXC= 1/ωC. Substituting and taking the common factor I gives:where Zseries is the series impedance: the ratio of the voltage to current in an RLC series ciruit. Note that, once again, reactances and resistances add according to Pythagoras' law: Zseries2 = R2 + Xtotal2
= R2 + (XL - XC)2. Remember that the inductive and capacitive phasors are 180° out of phase, so their reactances tend to cancel.Now let's look at the relative phase. The angle by which the voltage leads the current is φ = tan-1 ((VL - VC)/VR). Substiting VR = IR, VL = IXL = ωL and VC = IXC= 1/ωC gives:The dependence of Zseries and φ on the angular frequency ω is shown in the next figure. The angular frequency ω is given in terms of a particular value ωo, the resonant frequency* (ωo2 = 1/LC), which we meet below. * Again, let's check the units: L (flux per unit current) is in henrys = tesla.m2/ampere, and Faraday's law gives volts = tesla.metre2/second, so L is in volt.second/ampere = volt.second2/coulomb. C (charge per unit voltage) is in farads (coulomb/volt), so LC has the units of (volt.second2/coulomb)(coulomb/volt) = second2. (Setting the inductance term to zero gives back the equations we had above for RC circuits, though note that phase is negative, meaning (as we saw above) that voltage lags the current. Similarly, removing the capacitance terms gives the expressions that apply to RL circuits.)The next graph shows us the special case where the frequency is such that VL = VC. Because vL(t) and vC are 180° out of phase, this means that vL(t) = - vC(t), so the two reactive voltages cancel out, and the series voltage is just equal to that across the resistor. This case is called series resonance, which is our next topic.
ResonanceNote that the expression for the series impedance goes to infinity at high frequency because of the presence of the inductor, which produces a large emf if the current varies rapidly. Similarly it is large at very low frequencies because of the capacitor, which has a long time in each half cycle in which to charge up. As we saw in the plot of Zseriesω above, there is a minimum value of the series impedance, when the voltages across capacitor and inductor are equal and opposite, ie vL(t) = - vC(t) so VL(t) = VC, soωL = 1/ωC so the frequency at which this occurs is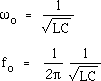
where ωo and fo are the angular and cyclic frequencies of resonance, respectively. At resonance, series impedance is a minimum, so the voltage for a given current is a minimum (or the current for a given voltage is a maximum).| This phenomenon gives the answer to our teaser question at the beginning. In an RLC series circuit in which the inductor has relatively low internal resistance r, it is possible to have a large voltage across the the inductor, an almost equally large voltage across capacitor but, as the two are nearly 180° degrees out of phase, their voltages almost cancel, giving a total series voltage that is quite small. This is one way to produce a large voltage oscillation with only a small voltage source. In the circuit diagram at right, the coil corresponds to both the inducance L and the resistance r, which is why they are drawn inside a box representing the physical component, the coil. Why are they in series? Because the current flows through the coil and thus passes through both the inductance of the coil and its resistance. You get a big voltage in the circuit for only a small voltage input from the power source. You are not, of course, getting something for nothing. The energy stored in the large oscillations is gradually supplied by the AC source when you turn on, and it is then exchanged between capacitor and inductor in each cycle. For more details about this phenomenon, and a discussion of the energies involved, go to LC oscillations. |
|
Bandwidth and Q factorAt resonance, the voltages across the capacitor and the pure inductance cancel out, so the series impedance takes its minimum value: Zo = R. Thus, if we keep the voltage constant, the current is a maximum at resonance. The current goes to zero at low frequency, because XC becomes infinite (the capacitor is open circuit for DC). The current also goes to zero at high frequency because XL increases with ω (the inductor opposes rapid changes in the current). The graph shows I(ω) for circuit with a large resistor (lower curve) and for one with a small resistor (upper curve). A circuit with low R, for a given L and C, has a sharp resonance. Increasing the resistance makes the resonance less sharp. The former circuit is more selective: it produces high currents only for a narrow bandwidth, ie a small range of ω or f. The circuit with higher R responds to a wider range of frequencies and so has a larger bandwidth. The bandwidth Δω (indicated by the horiztontal bars on the curves) is defined as the difference between the two frequencies ω+ and ω- at which the circuit converts power at half the maximum rate.Now the electrical power converted to heat in this circuit is I2R, so the maximum power is converted at resonance, ω = ωo. The circuit converts power at half this rate when the current is Io/√2. The Q value is defined as the ratio | 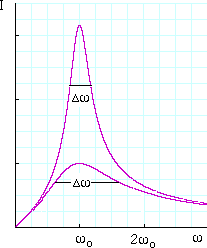
|
Complex impedanceYou have perhaps been looking at these phasor diagrams, noticing that they are all two-dimensional, and thinking that we could simply use the complex plane. Good idea! But not original: indeed, that is the most common way to analyse such circuits.The only difference from the presentation here is to consider cosusoids, rather than sinusoids. In the animations above, we used sin waves so that the vertical projection of the phasors would correspond to the height on the v(t) graphs. In complex algebra, we use cos waves and take their projections on the (horizontal) real axis. The phasor diagrams have now become diagrams of complex numbers, but otherwise look exactly the same. They still rotate at ωt, but in the complex plane. The resistor has a real impedance R, the inductor's reactance is a positive imaginary impedance and the capacitor has a negative imaginary impedanceConsequently, using bold face for complex quantities, we may write:Zseries = (R2 + (jωL + 1/jωC)2)1/2 and so on. The algebra is relatively simple. The magnitude of any complex quantity gives the magnitude of the quantity it represents, the phase angle its phase angle. Its real component is the component in phase with the reference phase, and the imaginary component is the component that is 90° ahead.
There are pages on related material atA good text book is: Introductory Alternating Current Circuit Theory, by G.J. Russell and K. Mann, UNSW Press, 1990.
We're still working on this page and shall add more to it as time permits.
Happy birthday, theory of relativity!As of June 2005, relativity is 100 years old. Our contribution isEinstein Light: relativity in brief... or in detail. It explains the key ideas in a short multimedia presentation, which is supported by links to broader and deeper explanations. | |
|





